Matched Filters – Three Ways of Solving for the Output
$5.00
This document contains multiple solutions to some of the more difficult matched filter problems found in an undergraduate course on Communication Systems. This document details how to find the output of a matched filter by way of three methods: analytical convolution, graphical convolution, and convolution with Laplace Transforms. It is pure preference as to how you decide to convolve two functions; however, depending on the functions being convolved, one method may prove more suitable than another.
Besides evaluating a few integrals and taking some Laplace Transforms, the majority of the math contained in this document is algebra. There are many tools available you can use to simplify the mathematics you are about to read. As always, it is a great practice to solve for the solution by hand, and verify your solution using a tool like MATLAB. This not only strengthens your algebraic abilities, but also enhances your programming skills, which are both very important for engineering students.
Solutions to the problems depicted below are contained within this document.
Description
Excerpt from the document:
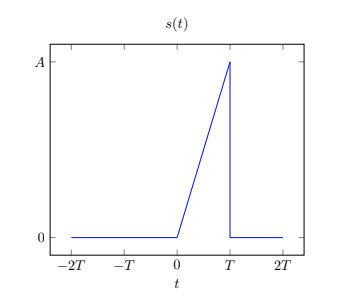
Write out \(s(t)\) and \(h(t)\) in terms of a function that turns on at time \(t = 0\) and turns off at time \(t = T\):
\begin{equation*}
\begin{split}
& s(t) = \frac{A}{T}t[u(t) – u(t-T)]\\
& h(t) = (A – \frac{A}{T}t)[u(t) – u(t-T)]
\end{split}
\end{equation*}
Determine the function, \(s(t)\) or \(h(t)\), that is to be the shifter. The shifter is the function that will replace \(t\) with \(t-\tau\) for all \(t\) within the function. Generally, pick the function that is the easiest to interpret/has the least amount arguments within the function. For Example 1, choose the shifter to be \(s(t)\).
Rewrite \(s(t)\) as \(s(t-\tau)\) and \(h(t)\) as \(h(\tau)\):
\begin{equation*}
\begin{split}
s(t-\tau) & = \frac{A}{T}(t-\tau)[u(t-\tau) – u(t-\tau-T)]\\
h(\tau) & = (A – \frac{A}{T}\tau)[u(\tau) – u(\tau-T)]
\end{split}
\end{equation*}
Our integrand is equal to \(s(t-\tau)h(\tau)\). We will evaluate the integrand with respect to \(\tau\) between the limits of \(-\infty\) to \(+\infty\).



Reviews
There are no reviews yet.