BJT Amplifiers – Small Signal Analysis

Description

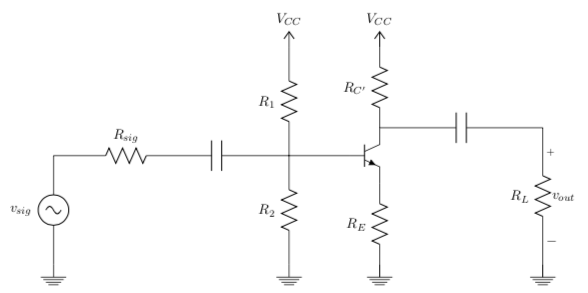
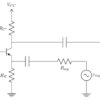
Excerpt from the Common Emitter section of document (depicted in main image of this resource):

The first figure of merit we are asked to determine is $R_{in}$.

We know from Figure 5 that $R_{in}$ represents the entire amplifier to the right of $R_{sig}$. We also know that $R_{in} = \frac{v_{in}}{i_{in}}$. We can determine $v_{in}$ and $i_{in}$ from the circuit in Figure 10.

Writing a nodal equation for $i_{in}$ yields:

$$\begin{align} i_{in} &= i_{B} + i_{b} \nonumber \\ \textit{where } i_{B} &= \frac{v_{in}}{R_{B}} \nonumber \\ i_{in} &= \frac{v_{in}}{R_{B}} + i_{b}\ \ \ \ \ (2) \end{align}$$

Writing a mesh equation for $v_{in}$ yields:

$$\begin{equation} v_{in} = i_{b}r_{\pi} + i_{e}R_{E}\ \ \ \ \ (3) \end{equation}$$

Let’s continue to develop $v_{in}$ by obtaining it in terms of $i_{b}$ since Equation (2) is in terms of $i_{b}$. We can accomplish this by writing a nodal equation for $i_{e}$, where:

$$\begin{align} i_{e} &= i_{b} + \beta{i_{b}} \nonumber \\ &= (\beta+1)i_{b}\ \ \ \ \ (4) \end{align}$$

Subbing $i_{e}$ in Equation (4) for $i_{e}$ in Equation (3) yields:

$$\begin{align} v_{in} &= i_{b}r_{\pi} + i_{b}(\beta+1)R_{E} \nonumber \\ &= [r_{\pi} + (\beta+1)R_{E}]i_{b}\ \ \ \ \ (5) \end{align}$$

Solving for $i_{b}$ in Equation (5) produces:

$$\begin{equation} i_{b} = \frac{v_{in}}{r_{\pi} + (\beta+1)R_{E}}\ \ \ \ \ (6) \end{equation}$$

Substituting Equation (6) into Equation (2) for $i_{b}$ yields:

$$\begin{align} i_{in} &= \frac{v_{in}}{R_{B}} + \frac{v_{in}}{r_{\pi} + (\beta+1)R_{E}} \nonumber \\ &= \left[\frac{1}{R_{B}} + \frac{1}{r_{\pi} + (\beta+1)R_{E}}\right]v_{in}\ \ \ \ \ (7) \end{align}$$

Solving for $\frac{i_{in}}{v_{in}}$ in Equation (7) yields:

$$\begin{equation} \frac{i_{in}}{v_{in}} = \frac{1}{R_{in}} = \frac{1}{R_{B}} + \frac{1}{r_{\pi} + (\beta+1)R_{E}}\ \ \ \ \ (8) \end{equation}$$

From circuit theory, we know that:

$$\begin{equation*} \frac{1}{R_{Parallel}} = \frac{1}{R_{x}} + \frac{1}{R_{y}} \end{equation*}$$

With this knowledge we obtain $R_{in}$ from Equation (8) as:

$\newcommand{\parallelsum}{\mathbin{\!/\mkern-5mu//\!}}$
$$\begin{equation} \boxed{R_{in} = R_{B}\parallelsum[r_{\pi} + (\beta+1)R_{E}]}\ \ \ \ \ (9) \end{equation}$$

The next figure of merit we are asked to find is the Open Circuit Voltage Gain, $A_{v_o}$.

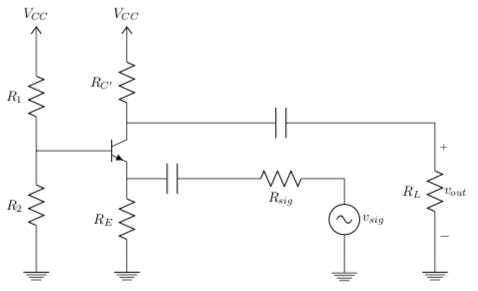
We can determine $v_{out}$ by inspecting the right side of the circuit in Figure 10.

$$\begin{equation} v_{out} = -\beta{i_{b}}R_{C} \ \ \ \ \ (10) \end{equation}$$

Taking Equation 10 and dividing it by Equation 5 gives us:

$$\begin{align} \frac{v_{out}}{v_{in}} &= \frac{-\beta{i_b}R_{C}}{[r_{\pi} + (\beta+1)R_{E}]i_{b}} \nonumber \\ &= \boxed{\frac{-\beta R_{C}}{r_{\pi} + (\beta+1)R_{E}} = A_{v_o}}\ \ \ \ \ (11) \end{align}$$

We were also asked to find the Overall Circuit Voltage Gain, $\frac{v_{out}}{v_{sig}}$.

We can do this by substituting $v_{in}$ within Equation (1) for $v_{in}$ within Equation (11).

$$\begin{align} \frac{v_{out}}{\frac{R_{in}}{R_{in}+R_{sig}}v_{sig}} &= \frac{-\beta R_{C}}{r_{\pi} + (\beta+1)R_{E}} \nonumber \\ \frac{v_{out}}{v_{sig}} &= \boxed{\left(\frac{-\beta R_{C}}{r_{\pi} + (\beta+1)R_{E}}\right)\left(\frac{R_{in}}{R_{in}+R_{sig}}\right)}\ \ \ \ \ (12) \end{align}$$

The last figure we are asked to determine is the output resistance, $R_{out}$, which is simply:

$$\begin{equation*} \boxed{R_{out} = R_{C’}} \end{equation*}$$

Remember from Section 2.3 that we find $R_{out}$ by looking into the terminal where $R_L$ is connected and as it approaches $\infty$. We can easily see that $R_{out} = R_{C’}$ from Figure 11.